Percentages: Formulas, Tricks and Shortcuts

The following is a list of important formulas for Percentage:

1. Percent implies “for every hundred”.
% is read as percentage and x % is read as x per cent.

2. To calculate p % of y
(p/100) x y = (p x y)/100

p % of y = y % of p

3. To find what percentage of x is y: y/x × 100

4. To calculate percentage change in value
Percentage change = {change/(initial value)} x 100

5. Percentage point change = Difference of two percentage figures

6. Increase N by S % = N( 1+ S/100 )

7. Decrease N by S % = N (1 – S/100)

8. If the value of an item goes up/down by x%, the percentage reduction/increment to be now made to bring it back to the original point is 100x/ (100 + x) %.

9. If A is x% more /less than B, then B is 100x/(100 + x) % less/more than A.

10. If the price of an item goes up/down by x %, then the quantity consumed should be reduced by 100x/ (100 + x)% so that the total expenditure remains the same.

11. Successive Percentage Change
If there are successive percentage increases of a % and b%, the effective percentage increase is:
{(a + b + (ab/100)}%

12. Percentage – Ratio Equivalence:

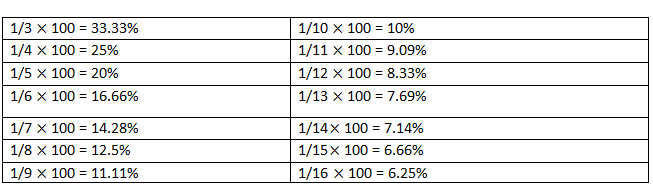
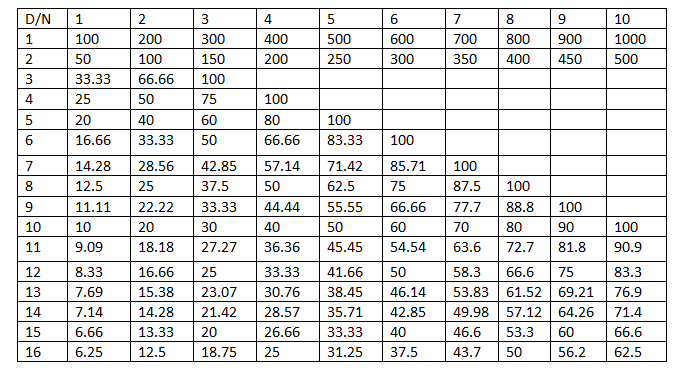
N is Numerator
D is the Denominator

13. Product Stability Ratio:
A × B = P
If A is increased by a certain percentage, then B is required to be decreased by a certain percentage to keep the product P stable.

Expressing the percentage figures in ratios:

Percentages: Types of Problems/Questions-1

Problem Type-1:

If a reduction of p % in the price of an article enables a person to buy y kg more for Rs R,then we can arrive at the following results:
Reduced price=> Rp/100y per kg
Original prices per kg= Rp/(100-p)y per kg

Example: A reduction of 21% in the price of an item enables a person to buy 3 kg more for 100. Thereduced price of item per kg is:
(a) Rs. 5.50
(b) Rs. 7.50
(c) Rs. 10.50
(d) Rs. 7.00

Solution:(d)
Reduced price will be:
Rp/100y per kg
In our case R= Rs. 100 , x=21% , y=3kg
{(100 x 21)/(100 x 3)} = Rs. 7
Alternate method:Expenditure = price per quantity × consumption
E = P × Q =100……. (1)
Now, as per the question,

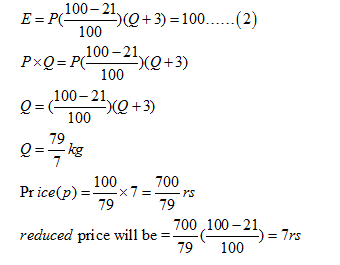
Problem Type-2: Problems based on mixtures

Example: A vessel has 60 L of solution of acid and water having 80% acid. How much water is to be added to make it solution in which acid forms 60%?
(a) 48 L
(b) 20 L
(c) 36 L
(d) None of these

Solution: (b)
Given, percentage of acid = 80%
Then, percentage of water = 20%
In 60L of solution, water = (60 x 20)/ 100 = 12L
Let p liter of water is to be added.
According to the question,
=>{(12 + p)/(60 + p)} x 100 = 40  (∵   100 – 60 = 40% water)
=>1200 + 100p = 2400 + 40p
⇒ 60p = 1200
p= 20L

Problem Type-3: Problems based on Ratios and Fractions
Example: If the numerator of a fraction is increased by 20% and the denominator is decreased by 5%, the value of the new fraction become 5/2. The original fraction is:
(a) 24/19
(b) 3/18
(c) 95/48
(d) 48/95

Solution: (c)
Let original fraction be p/y
According to the question,
{(120/100)p/(95/100)y} = 5/2
120p/95y = 5/2
=> p/y = (5/2)x (95/120) = 95/48.

Problem Type-4: Problems based on Income, salary, expenditure

Example:The monthly income of a person was Rs 13500 and his monthly expenditure was Rs 9000. Nextyear his income increased by 14% and his expenditure increased by 7%. The per cent increase inhis savings was:
(a) 7%
(b) 21%
(c) 28%
(d) 35%

Solution: (c)
Given, monthly income = 13500 and expenditure = 9000
Then, original savings= Rs. (13500-9000) = Rs 4500
New income = 114% of Rs. 13500 = Rs 15390
New expenditure= 107% of Rs 9000 = Rs 9630
New saving = Rs. (15390 – 9630) = Rs 5760
NS = new savings
OS = Original savings
Percentage increase in savings = {(NS – OS)/OS} X 100
{(5760 – 4500)/4500} X 100 = (1260/4500)X 100 = 28%